Special right triangles - Basic concepts and examples
This article will be about the special right triangles, and the 3 most common special right triangles, with examples.
What are the special right triangles
The special right triangles are triangles that have some established characteristics that allows us to find the sides and angles of the triangle only by taking as reference the proportions of the sides and angles without the need of using the traditional formulas like the trigonometric ratios or the Pythagorean theorem.
The special right triangles uses the proportions between the relations of the sides and angles of a right triangle. The length of the sides of a triangle cannot be found if we only know the angles, but with the angles we can define the proportion that each side will have, for example, if we have a triangle that has certain angles, based on that we can define that the triangle will have a side that will be 5 units long, other one that will be 4 units long, and the third one will be 3 units long, and this is the basic principle of the special right triangle, not knowing the exact length of the sides of a triangle but knowing the proportions that the sides will have.
General properties of the triangles
A reminder before we continue, to name the sides and angles of a triangle, normally we use the letters A, B and C, where the capital letters are used to name the angles and the lowercase letters are used to name sides, where the sides are going to have the same name as the opposite angle. Another thing important to say is that the bigger the angle is, the longer the opposite side will be.
Another aspect to be clear when we work with special right triangles is that the sum of the three angles will be equals to 180, but as we already know a right triangle has a 90° angle, this means that the sum of the other 2 angles will be equals to 90°, this is why when we know the value of an angle we can easily find the other angle just by subtracting the angle we know to 90°.
In this triangles we are going to be using the letter “k” indicating a proportion, for example, if we have the sides “1k” and “2k”, we can see that the “2k” side is double the length of the “1k” side, so this is not the actual length of the side but it is the proportion based on the length of the other side.
Special right triangles
There is a big amount of special right triangles, but in general the most common are the following.
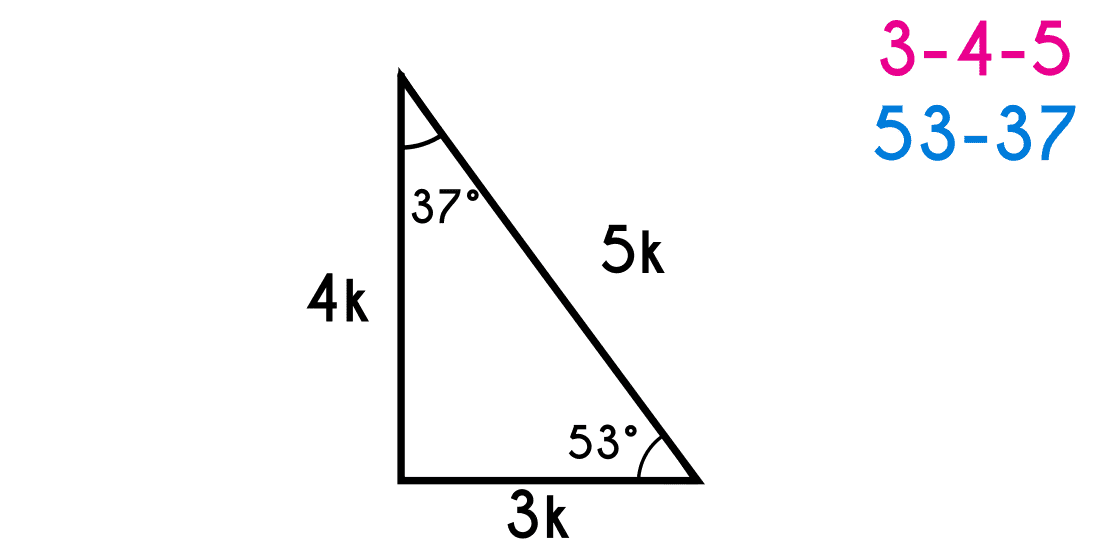
Triangle 37-53(angles) or 3-4-5(sides).
This triangle has a 37° angle and the other angle is 53° where the opposite side to the 37° angle will be 3k, the opposite side to the 53° angle will be 4k and the hypotenuse will be 5k.
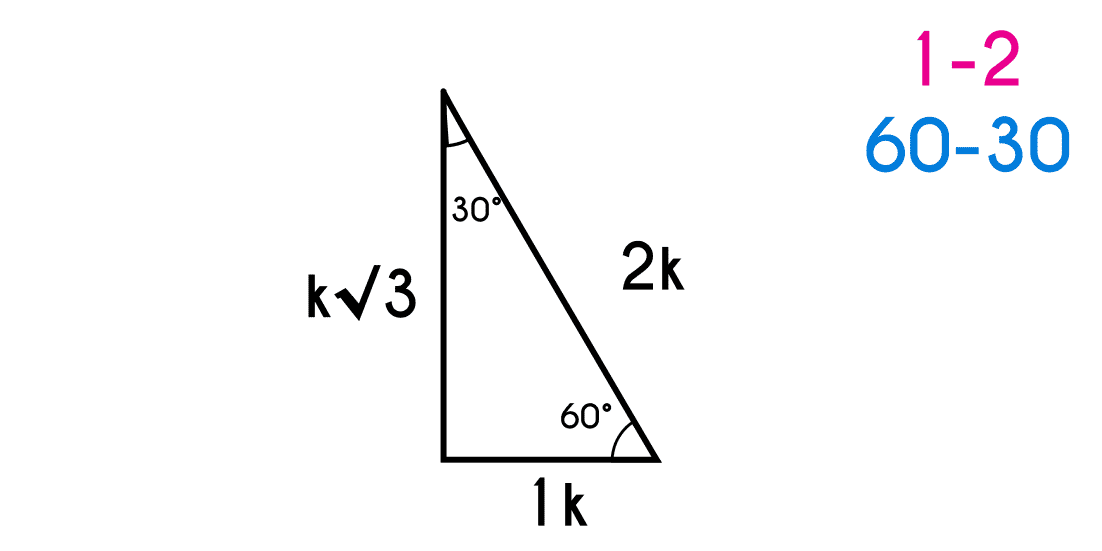
Triangle 30-60(angles) or 1-2(sides).
This triangle has one 30° angle and a 60° angle, where the opposite side to the 30° angle will be 1k, and the opposite side to the 60° angle will be k√3 and the hypotenuse will be 2k (this means that the hypotenuse will be twice as long as the 1k side).
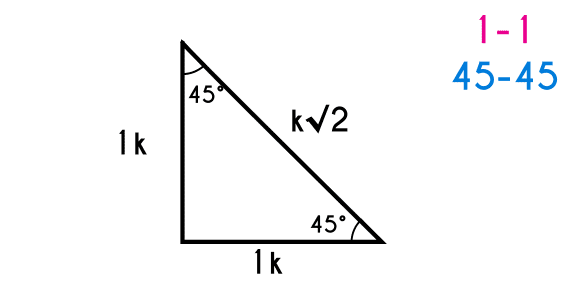
Triangle 45-45(angles) or 1-1(sides)
In this triangle there are 2 45° angle, so the two legs are going to have the same length “1k”, while the hypotenuse will be k√2.
Examples using the special right Triangles
Example 1: Find the remaining sides of the following triangle that has one angle of 30°
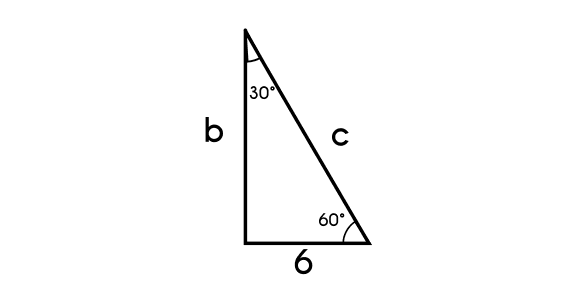
As you can see in the image above this is a 30-60 triangle, and the given side is the opposite side to the 30° angle, it means that this side will be the 1k side, so the other two sides will be the k2 (c) and the k√3 (b).
- In this case the side given is the “1k” side, so the value of k will be equals to 6.
- k = 6
- Now that we know the “k” value we´ll find the “b” side (k√3)
- b = k√3
- b = 6√3
- b = 10.39
- and then the “c” side (2k)
- c = 2k
- c = 2(6)
- b = 12
Example 2: Find the three remaining sides of the following triangle that has a 53° angle which hypotenuse is 25.
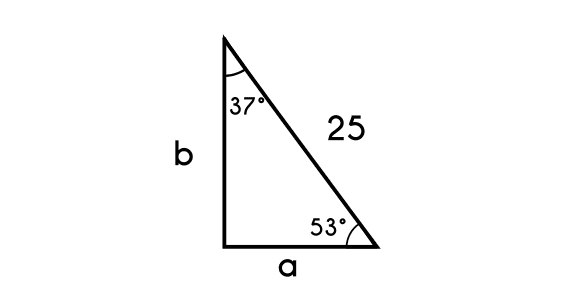
This is a 53-37 and the side of 25 is the 5k side
- First we find the value of “k”
- 5k = 25
- k = 25 / 5
- k = 5
- Then we find the b side (4k)
- b = 4k
- b = 4(5)
- b = 20
- and last we find the c side (3k)
- c = 3k
- c = 3(5)
- b = 15
Example 3:Complete this triangle
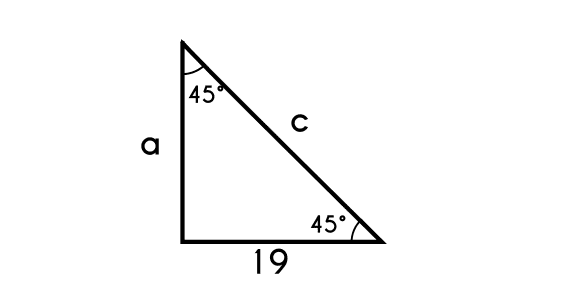
The triangle in this example is a 45-45 and the given value (19) is the 1k side, this triangle is known for having the legs of equals length, so the only thing left here is to find the hypotenuse.
- First we find the value of "k"
- 1k = 19
- k = 19
- and we find the other leg
- a = 1k
- a = 19
- and finally we find the hypotenuse c (k√2)
- c = k√2
- c = 19√2
- c = 26.87
Example 4:find the remaining sides of the next triangle 30-60
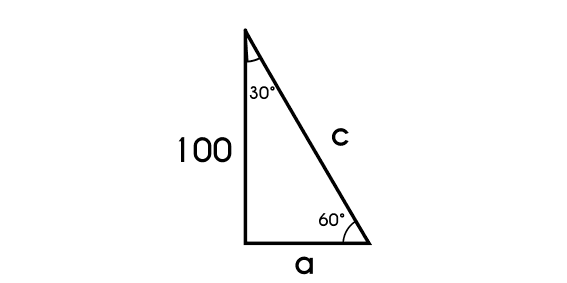
the side we have is the k√3
- First we find the k value
- k√3 = 100
- k = 100 / √3
- k = 57.74
- then we find the a side
- a = 1k
- a = 57.74
- and we find the hypotenuse 2k
- c = 2k
- c = 2 (57.74)
- c = 115.48
Example 5: Find every side of this triangle 37-53
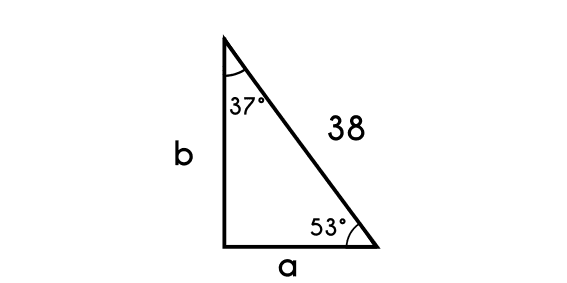
The side we know is the 5k
- First we find the k value
- 5k = 38
- k = 38 / 5
- k = 7.6
- Then we find the b side
- b = 4k
- b = 4(7.6)
- b = 30.4
- and finally we find the other side (3k)
- a = 3k
- a = 3 (7.6)
- a = 22.8
Related articles