Función lineal

En este artículo, se explicará el concepto principal de la función lineal, cómo diferenciar este tipo de función y cómo establecerlas con ejemplos.

Definición de una función lineal

La función lineal es un tipo de función que tiene la forma f(x) = mx + b o y = mx + b. Esta función también es conocida como función de primer grado, haciendo referencia a que la variable independiente, por lo general "x," está elevada a la primera potencia (x¹).

La principal característica de una función lineal es que tiene un crecimiento constante en toda la función. Esto significa que su rango avanza a la misma velocidad todo el tiempo.

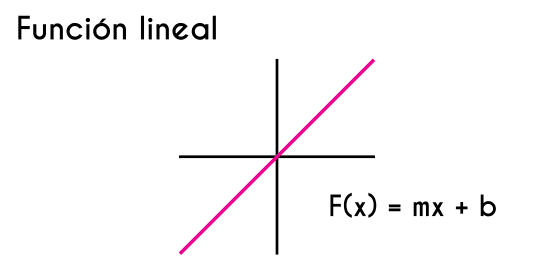
Cuando se grafica una función lineal, se obtiene una línea recta que tiene cierto ángulo de inclinación con respecto al eje de las "x". Si una recta no tiene este ángulo de inclinación, entonces se estaría hablando de una función constante en lugar de una función de primer grado.

A una función lineal también se le conoce como "recta", haciendo referencia a la forma que tiene su gráfica, que es una línea recta. Por lo tanto, cuando se escuche hablar de "rectas paralelas," "pendiente de una recta" o cualquier tema relacionado con las rectas, se debe saber que se está hablando de una función lineal.

Como se enseñó anteriormente, la forma general de la función es f(x) = mx + b. Aunque la forma general de la función sea esta, no tiene que ser escrita estrictamente de esta manera. En este caso, "b" es un número cualquiera que puede o no estar representado en la ecuación de la función. En caso de estarlo, entonces "b" tomará el valor del número que esté en su posición, pero en caso de no haber ningún número en el lugar de "b," entonces se entiende que el valor de "b" es igual a 0. Esto aplica de la misma manera con la variable "m," de la cual se hablará a continuación.

La función lineal y su aplicación en la vida cotidiana y profesional

La función lineal es un concepto fundamental que tiene una amplia aplicabilidad en la vida cotidiana y en numerosas profesiones. En situaciones cotidianas, como el cálculo de costos, la planificación de rutas o la predicción de tendencias, la función lineal desempeña un papel esencial.

En el ámbito profesional, la función lineal es crucial en campos como la física, la economía, la ingeniería y la estadística. En física, se utiliza para describir relaciones lineales entre variables, como la velocidad en función del tiempo. En economía, se modelan relaciones de costos y beneficios. En ingeniería, se aplica en diseño y análisis de sistemas lineales. Además, en estadística, se emplea para ajustar modelos lineales a datos observados.

El conocimiento de las propiedades de la función lineal es esencial para analizar y resolver problemas en estas áreas, lo que demuestra su relevancia en la vida cotidiana y en una amplia gama de profesiones.

Características de la función lineal

La función lineal se caracteriza por su forma específica y propiedades únicas. Esta función se expresa matemáticamente como f(x) = mx + b, donde "m" es la pendiente y "b" es el término independiente.

Uno de los aspectos clave de la función lineal es que cruza ambos ejes, x e y, en puntos definidos. El punto de corte con el eje x se llama "abscisa" y ocurre cuando "y" es igual a cero. El punto de corte con el eje y se denomina "ordenada al origen" y sucede cuando "x" es igual a cero. Estos puntos de corte son fundamentales para entender la función lineal y su comportamiento.

Una característica interesante de la función lineal es que no tiene límite. A medida que "x" se acerca al infinito o al menos infinito, la función también se extiende hacia el infinito en ambas direcciones. Esta propiedad la diferencia de otras funciones que pueden tener límites definidos.

Pendiente de una función lineal

La pendiente de una función lineal se representa con la letra "m" y esto indica qué tan inclinada es la gráfica y define el crecimiento de una función. Ojo, esto no es un ángulo de inclinación; este valor representa el avance que tiene "y" por cada aumento de valor en "x." La pendiente de una función puede ser escrita tanto como un número entero como una fracción.

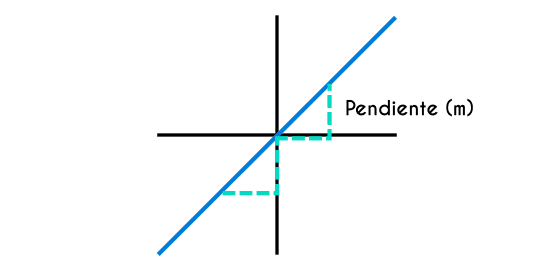
Se puede interpretar fácilmente el comportamiento de una función lineal simplemente basado en su pendiente "m." Si la pendiente es un número entero, entonces ese número representará el avance que tendrá en "y" por cada número en "x. Por ejemplo, si la pendiente de una función es igual a 4, entonces por cada valor que se incremente en "x," avanzará 4 en "y."

En caso de que la pendiente de la recta sea una fracción (m = a/b), entonces esto se interpretará así: por cada "b" valores que se incremente en "x," se incrementa "a" en y. Por ejemplo, si la pendiente de una función es m = 2/6, entonces por cada 6 números que avance "x," la función avanzará 2 en "y."

Mientras más alto sea el valor de la pendiente, más inclinada será la recta de la función, y mientras más cercana a 0 sea la pendiente, más plana será la función lineal.

El signo que esté antes de la pendiente también influye en la función, pues si el signo de la pendiente es negativo (-m), entonces la función será decreciente. Esto quiere decir que la función irá decayendo a medida que avanza en "x". En cambio, si el signo de la pendiente es positivo (+m o simplemente "m"), entonces la función irá creciendo conforme avancen los valores de "x."

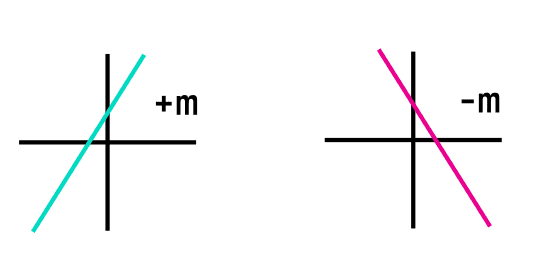
Punto de corte con el eje y de una función lineal

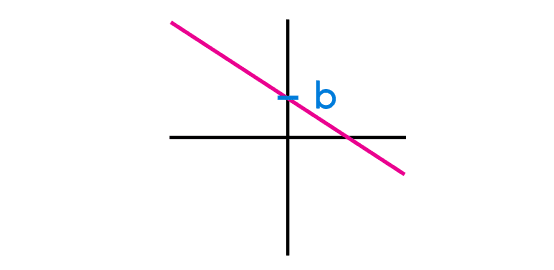
Otra variable que se puede observar en la forma de la recta es "b". "b" es el número que no está acompañado de la variable "x". En caso de no haber un número solo, entonces "b" es 0. El valor de "b" representa el punto de corte con el eje "y". Esto significa que si "b" vale 2, entonces la función cortará con el eje "y" cuando "y" valga 2. En caso de que "b" sea igual a 0, entonces el punto de corte de la función con el eje "y" será en y=0. Aparte de esto, otro aspecto que hay que tener en cuenta es que cualquier función corta con el eje "y" cuando "x" es igual a 0.

Dominio y rango de una función lineal

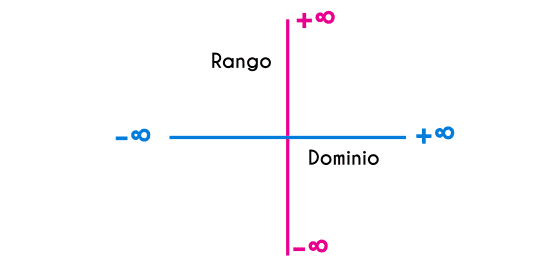
Tanto el dominio como el rango de una función lineal son los números reales. Esto, representado en intervalos, sería desde menos infinito hasta más infinito: ]-∞ , +∞[. Esto será en cualquier función lineal, no importa si la pendiente de la función es muy plana, al final siempre tenderá hacia infinito en ambos lados de la función.

Historia de la Función Lineal

La función lineal es uno de los conceptos fundamentales en matemáticas y tiene una historia que se remonta a la antigua Grecia. Matemáticos como Euclides y Apolonio comenzaron a investigar las propiedades de las líneas y sus relaciones con las ecuaciones en ese período.

Sin embargo, el desarrollo formal de las funciones lineales como las conocemos hoy en día se produjo durante el Renacimiento y la Edad Moderna. Matemáticos como René Descartes y Pierre de Fermat desempeñaron un papel crucial al introducir sistemas de coordenadas cartesianas y representar las relaciones matemáticas mediante ecuaciones algebraicas.

En el siglo XVII, el matemático francés Blaise Pascal contribuyó significativamente al estudio de las propiedades de las funciones lineales y al desarrollo de métodos para resolver problemas relacionados con el cálculo de áreas bajo curvas. Esta época marcó el inicio del análisis matemático moderno y la formalización de las funciones lineales como una parte esencial de las matemáticas.

Con el tiempo, el estudio de las funciones lineales se ha convertido en un componente fundamental de la educación matemática y se aplica en una amplia variedad de campos, incluyendo la física, la economía, la ingeniería y la estadística. La función lineal sigue siendo un concepto esencial en la resolución de problemas y la comprensión de relaciones matemáticas en el mundo moderno.

En la vida cotidiana existen varias situaciones donde se puede observar una función lineal, como el porcentaje de bateria de un teléfono celular que se está cargando, la cantidad de pasos que una persona da cuando camina etc. hay un sin fin de situaciones donde se pueden observar este tipo de funciones, a continuación se plantearán y desarrollarán algunos ejemplos de funciones lineales.

Ejemplo 1: Una persona va corriendo en un parque a un paso constante y se sabe que está persona va avanzando 2 metros por cada segundo que pasa.

Gran parte de las funciones aplicadas a problemas reales es el planteamiento de las misma, así que lo que primero se hará es plantear la función.

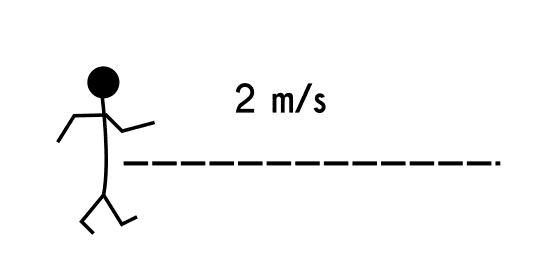
Lo primero que hay que hacer para plantear una función es determinar cuál es la variable dependiente y cuál es la variable independiente del planteamiento.

En este caso si se lee y se analiza el problema se nota que hay 2 variables, una es los metros que la persona recorre y la otra es el tiempo, en casos donde se ve involucrado el tiempo, se sabe que este es siempre la variable independiente y que todas las demás variables cambian con respecto a el, en este caso la otra variable, es decir los metros recorridos aumentan dependiendo del tiempo que pase.

Entonces ya se sabe que el tiempo será el dominio de la función y los metros serán el rango de la función, entonces se puede plantear ya la ecuación de la función.

Cómo la distancia aumenta en 2 valores por cada uno del tiempo, entonces la función para este supuesto sería f(t) = 2t, donde “t” representa el tiempo y f(t) son los metros que avanza la persona que va corriendo.

Ahora que se tiene la función se puede calcular la cantidad de metros que recorre la persona en cualquier cantidad de tiempo simplemente evaluando la función, así como se muestra en el siguiente cuadro.

• Pasados 1s
• f(1) = 2(1)
• f(1) = 2
• Pasados 3s
• f(3) = 2(3)
• f(3) = 2
• Pasados 6s
• f(6) = 2(6)
• f(6) = 12
• Pasados 10s
• f(10) = 2(10)
• f(10) = 20

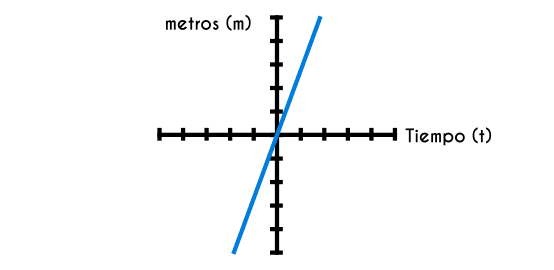
Ahora al tener ya la función, se puede graficar la cantidad de metros recorridos de la persona.

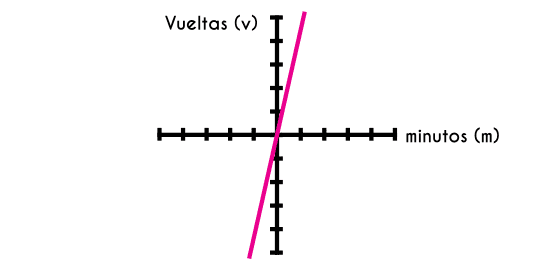
Ejemplo 2: Una rueda de feria da 4 vueltas por minuto, elaborar una función en este escenario.

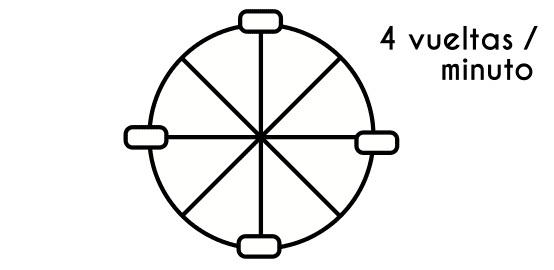
Este ejemplo se desarrollará con mayor rapidez. La variable independiente de esta función seguirá siendo el tiempo, solo que en este caso el tiempo estará medido en minutos en lugar de segundos y la variable dependiente evidentemente serán las vueltas que de la noria (rueda de feria).

Al escribir la función queda de la siguiente manera f(m) = 4m donde “m” representa los minutos transcurridos y f(m) es la cantidad de vueltas que ha dado la rueda de feria, esta función graficada quedaría de la siguiente manera.

Conclusión

La función lineal es un concepto matemático fundamental con una rica historia y una amplia aplicabilidad en la vida cotidiana y en diversas profesiones. Desde sus raíces en la antigua Grecia hasta su desarrollo en la Edad Moderna, las funciones lineales han desempeñado un papel esencial en la evolución de las matemáticas y en la comprensión de las relaciones numéricas y geométricas.

Hoy en día, el conocimiento de las características de la función lineal, como la pendiente y los puntos de corte, es crucial en campos tan diversos como la física, la economía, la ingeniería y la estadística. Estas funciones proporcionan herramientas poderosas para modelar y resolver problemas en una variedad de contextos.

En resumen, la función lineal es una piedra angular en las matemáticas y una herramienta valiosa en la resolución de problemas en el mundo real. Su estudio y comprensión son esenciales para cualquier persona que desee explorar las relaciones cuantitativas y aplicarlas en su vida cotidiana y en su carrera profesional.

Artículos relacionados