Ley de los cosenos
En este artículo se explicará la ley de los cosenos, con la definición principal de esta ley, la fórmula que se usa en problemas y ejemplos con su respectiva resolución
La ley de los cosenos es una fórmula que se usa para poder determinar los lados y ángulos de cualquier tipo de triángulo, pero esta ley principalmente se usa en triángulos oblicuángulos (triángulos que no tengan un ángulo de 90°), porque para triángulos rectángulos existen teoremas y razones que son específicamente para ese tipo de triángulos.
Existen 2 situaciones donde se puede hacer uso de la ley de los cosenos, una es cuándo se conoce la longitud de los 3 lados del triángulo, y la otra es cuándo se tiene 2 lados del triángulo y aparte se conoce el ángulo que forman estos 2 lados, estos 2 escenarios son los únicos donde se puede aplicar la ley de los cosenos.
Cuándo se utiliza la ley de los cosenos se va encontrando un dato a la vez (puede ser un ángulo o un lado), por lo que en ocasiones es necesario aplicar la ley de los cosenos en más de una sola vez para ir encontrando una por una las partes del triángulo que hagan falta.
Fórmula de la ley de los cosenos
La fórmula de la ley del coseno es solamente una, pero en el cuadro de abajo se muestran 3 variantes de la fórmula, en estas lo único que cambia es la posición de cada una de las variables, demostrando así que se puede encontrar cualquier lado o ángulo.
- c2 = a2 + b2 - 2 * a * b * cos(C)
- b2 = a2 + c2 - 2 * a * c * cos(B)
- a2 = b2 + c2 - 2 * b* c * cos(A)
En la ley de los cosenos se es muy común recurrir al despeje de una variable, por lo que es importante saber aunque sea las bases del despeje de variables, de todas formas, en los ejemplos que se realicen en este artículo se demostrará los despejes básicos que se usan en esta ley.
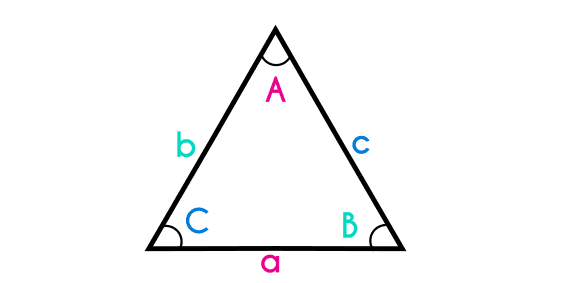
Algo que es importante recordar es el nombramiento de los ángulos y lados, por lo general tanto los ángulos y lados de un triángulo se nombran con los las primeras letras del abecedario, y tanto los lados y ángulos se nombran con los mismas letras, la diferencia está en que los lados se nombran con letras minúsculas (a, b y c) y los ángulos se nombran con letras mayúsculas (A, B y C), donde los lados del triángulo se nombran con la misma letra que el ángulo que esta en frente (el ángulo opuesto).
Lo anterior explicado es la forma que por lo general se utiliza, pero hay personas que tienen una diferente forma de nombrar los ángulos y lados de un triángulo, no por esto significa que está mal, pero la forma presentada aquí es la más simple y ayuda a no confundirse con la posición de los lados.
Ejemplos de la ley de los cosenos
Ejemplo 1: Hay un triángulo que tiene un lado “a” de 30 metros y otro lado “b” de 40 metros, si el ángulo que forman estos dos lados es de 23° de inclinación, encontrar la longitud del lado “c” que falta.
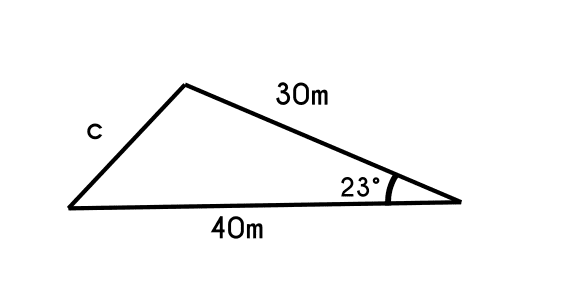
- Primero se establece la fórmula de la ley de los cosenos
- c2 = a2 + b2 - 2 * a * b * cos(C)
- En este caso no es necesario despejar nada, por lo que se cambian los datos directamente
- c2 = 302 + 402 - 2 * 30 * 40 * cos(23°)
- Y ahora se resuelven los procesos
- c2 = 2 500 - 2 400 * cos(23°)
- c2 = 2 500 - 2209.21
- c2 = 290.79
- c = √290.79
- c = 17.05
Ejemplo 2: Se tiene un triángulo el cual posee un ángulo “A” de 45°, si se sabe que los dos lados que forman son: “b” de 12cm y “c” de 22cm, calcular el otro lado “a” del triángulo.
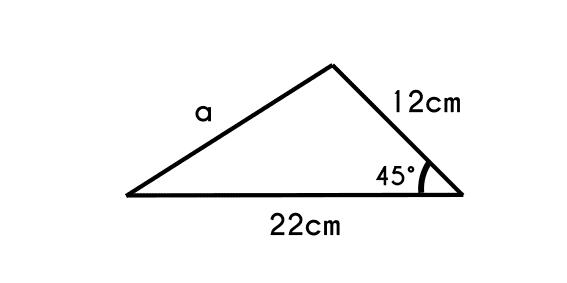
- Primero se escribe la ley de los cosenos con las variables a usar
- a2 = b2 + c2 - 2 * b * c * cos(A)
- Luego se cambian los datos y se resuelve
- a2 = 122 + 222 - 2 * 12 * 22 * cos(45)
- a2 = 144 + 484 - 373.35
- a2 = 254.65
- a = √254.65
- a = 15.96
Ejemplo 3: Calcular el angulo “C” de un triángulo que posee un lado a=20cm, b=23cm y c=10cm.
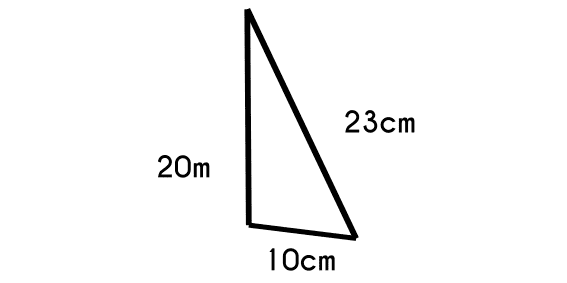
- Se escribe la ecuación
- c2 = a2 + b2 - 2 * a * b * cos(C)
- Ahora se despeja cos(C)
- c2 = a2 + b2 - ( 2 * a * b * cos(C) )
- c2 - a2 - b2 = - ( 2 * a * b * cos(C) )
- c2 - a2 - b2 = (- 2 * a * b ) * cos(C)
- cos(C) =
c2 - a2 - b2- 2 * a * b
- Ahora se cambian los datos y se resuelve
- cos(C) =
102 - 202 - 232- 2 * 20 * 23
- cos(C) =
100 - 400 - 529- 920
- cos(C) =
-829- 920
- cos(C) = 0.901
- C = cos-1(0.901)
- c = 25.71
Ejemplo 4: Cuál es la longitud del lado restante “g” de un triángulo que tiene 2 lados "e" y "f" de 30m cada uno y el ángulo que forman "G" estos dos lados es de 45°.
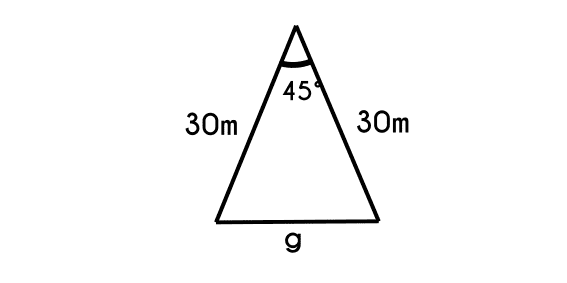
- Se plantea la ecuación
- g2 = e2 + f2 - 2 * e * f * cos(G)
- Ahora, como no es necesario hacer ningun despeje, se cambian los datos
- g2 = 302 + 302 - 2 * 30 * 30 * cos(45)
- g2 = 1 800 -1 272.79
- g2 = 1 800 -1 272.79
- g = √ 527.21
- g = 22.96
Ejemplo 5: Encontrar el todos los ángulos de un triángulo que tiene por lados: a=40cm, b=50cm y c=44cm.
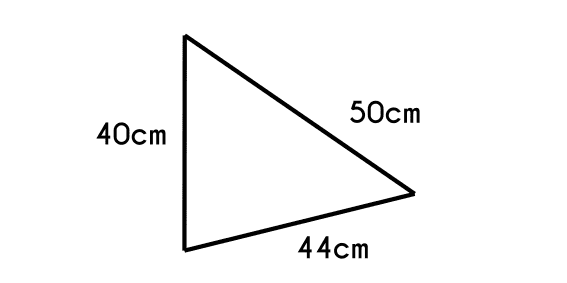
Primero se encontrará el ángulo C
- Se plantea la ecuación
- c2 = a2 + b2 - 2 * a * b * cos(C)
- Luego se despeja cos(C)
- c2 = a2 + b2 - ( 2 * a * b * cos(C) )
- c2 - a2 - b2 = - ( 2 * a * b * cos(C) )
- c2 - a2 - b2 = (- 2 * a * b ) * cos(C)
- cos(C) =
c2 - a2 - b2- 2 * a * b
- Ahora cambian los datos
- cos(C) =
442 - 402 - 502- 2 * 40 * 50
- cos(C) =
1 936 - 1 600 - 2 500- 4 000
- cos(C) =
-2 164- 4 000
- cos(C) = 0.541
- C = cos-10.541
- C = 57.25
Ahora se procederá a encontrar al ángulo B
- Se hace el mismo procedimiento que con el otro ángulo
- cos(B) =
b2 - a2 - c2- 2 * a * c
- Ahora cambian los datos
- cos(B) =
502 - 402 - 442- 2 * 40 * 44
- cos(B) =
2 500 - 1 600 - 1936- 3 520
- cos(B) =
-1 036- 3 520
- cos(B) = 0.2943
- B = cos-10.2943
- B = 72.88
Y por último se encuentra el ángulo A: se podria hacer usando la ley de los cosenos como se ha hecho con los otros ángulos, pero para que resulte más sencillo se encontrará usando los otros dos ángulos, como ya se sabe la suma de los tres ángulos interiores de un triángulo es 180, por lo que se encontrara usando este concepto
- A + B + C = 180
- A + 57.25 + 72.88 = 180
- A = 180 - 57.25 - 72.88
- A = 49.87