Función cuadrática
En este artículo, se dará la definición de las funciones cuadráticas, cada una de las partes que componen a este tipo de función, con fórmulas y ejemplos desarrollados.
Concepto de función cuadrática
La función cuadrática, también conocida como función de segundo grado, es una función que tiene la forma de f(x) = ax2 + bx + c. A este tipo de función se le denomina de segundo grado porque el máximo exponente que tiene la variable independiente en este tipo de funciones es 2.
La función cuadrática se caracteriza porque los valores del rango de la función bajan y luego de haber pasado por el centro de la función vuelven a subir, o viceversa; esto dependerá de la dirección de la función. Debido al comportamiento de la función cuadrática, al graficarla tiene una forma de "u" que se va abriendo y a esta forma se le conoce como parábola.
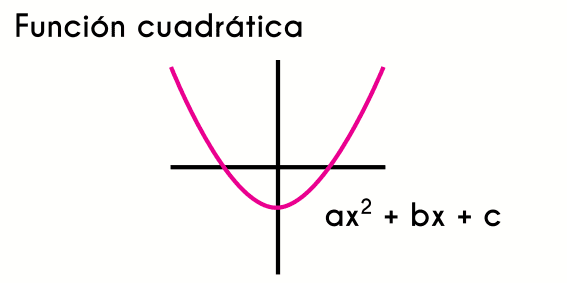
La ecuación de toda función cuadrática se divide en 3 partes que se les llamará términos. Estos términos son las constantes "a", "b" y "c", donde "a" será el número que se encuentra multiplicando (al lado) de "x2", "b" es el término que está multiplicando a "x" y "c" será el número que está solo. Algo que se aplica en cada término es que si no hay ningún número al lado de las variables "x2" o "x", entonces se intuye que el término de cada parte equivale a 1, porque cuando el valor del término es 1, por lo general este no se escribe; en cambio, cuando no hay ninguna "x" o un número solo, se entiende que el valor de cada uno de los términos es 0.
Por ejemplo, si se tiene la función f(x) = 6x2 + 3x, los términos de esta función son: a=6, b=3 y c=0, y en f(x) = x2 + 3, los términos de esta función cuadrática son: a=1, b=0 y c=3. Es necesario aprender a encontrar estos términos al ver la ecuación de la función porque sabiendo cada uno de los términos se puede graficar o encontrar el dominio y rango de cualquier función cuadrática sin necesidad de realizar procesos que pueden llegar a ser más tediosos y complejos.
Aplicaciones de la Función Cuadrática
La función cuadrática se encuentra en numerosos ámbitos cotidianos y profesionales debido a su versatilidad y capacidad para modelar una variedad de situaciones. Algunas de las aplicaciones comunes de las funciones cuadráticas en la vida cotidiana incluyen la modelización de trayectorias de proyectiles, el análisis de costos y beneficios en la economía, y la predicción de comportamientos en el mercado de valores. En el ámbito profesional, estas funciones se utilizan en campos como la ingeniería para diseñar estructuras y sistemas, en la física para describir movimientos y fuerzas, y en la biología para modelar el crecimiento de poblaciones.
Además, las funciones cuadráticas son ampliamente utilizadas en campos como la informática y la programación para resolver una variedad de problemas. En resumen, las aplicaciones de la función cuadrática son diversas y su comprensión es fundamental en numerosos aspectos de la ciencia y la ingeniería.
Características de la Función Cuadrática
Las funciones cuadráticas tienen varias características clave que son fundamentales para comprender su comportamiento:
- Forma General: La forma general de una función cuadrática es f(x) = ax2 + bx + c, donde "a", "b" y "c" son constantes.
- Vértice: El vértice de una parábola es el punto máximo o mínimo de la función, y se encuentra en el punto (h, k).
- Parábola: Las gráficas de las funciones cuadráticas tienen forma de parábola, que puede abrirse hacia arriba (si "a" es positivo) o hacia abajo (si "a" es negativo).
- Punto de Corte en el Eje X: El punto donde la parábola cruza el eje x se conoce como el punto de corte en el eje x o raíces. Pueden ser 0, 1 o 2 puntos según la discriminante (b2 - 4ac).
- Dominio y Rango: El dominio de una función cuadrática es el conjunto de todos los números reales. El rango depende de la dirección de apertura de la parábola y la posición del vértice.
Gráfica de la función cuadrática
La gráfica de una función cuadrática se caracteriza porque tiene forma de parábola. Esto significa que la gráfica va bajando hasta llegar a un punto en el que ya no baja, sino que al contrario comienza a ascender de nuevo, o viceversa. La gráfica va subiendo hasta llegar a su punto máximo y entonces empieza a bajar. Ojo, no todas las parábolas son funciones cuadráticas; solo se pueden considerar funciones a las parábolas verticales (que se abren o bien hacia arriba o bien hacia abajo), porque las parábolas horizontales no son funciones.
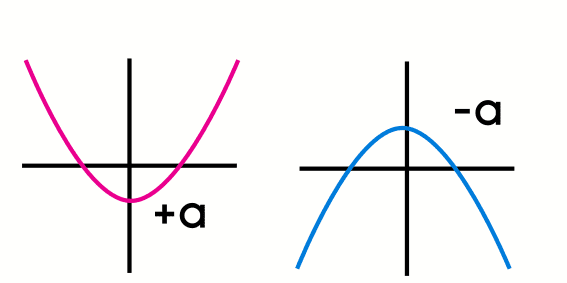
La dirección en la que abren las gráficas de las funciones cuadráticas va a depender del término "a". Si el término "a" es positivo, entonces la función cuadrática se abrirá hacia arriba; en caso contrario, si el término "a" es negativo, la parábola de la función cuadrática se abrirá hacia abajo. Por lo tanto, se puede determinar la forma de la función simplemente viendo la ecuación de la misma.
Por ejemplo, si se tiene la función f(x) = 4x2 + 2, esta función se abrirá hacia arriba; en cambio, la función f(x) = -x2 se abrirá hacia abajo.
Vértice de una función cuadrática
El vértice en una función cuadrática es el punto más alto (si la parábola abre hacia abajo) o es el punto más bajo (si la parábola abre hacia arriba) de la gráfica de la función en el eje "y". El vértice es también el punto medio de la parábola en el eje "x" y este divide a la función en 2.
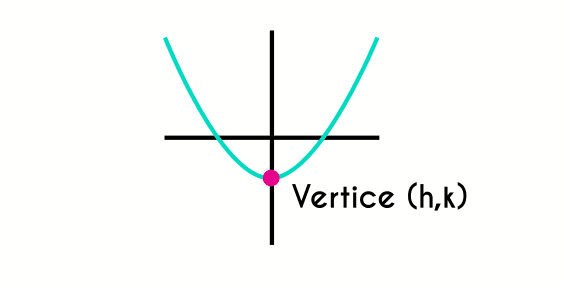
Para encontrar las coordenadas del vértice, se debe saber que las coordenadas de este se escriben de la forma (h, k), donde "h" es la coordenada en "x" del vértice y "k" es la coordenada en "y". Se escriben de esta manera para no confundirse con la forma de la función.
Para definir la ubicación del vértice se hace uso de unas fórmulas en las que se usan los términos de la función.
- h = -b2a
- k = f(h)
Como se puede observar en las fórmulas para encontrar la coordenada "k", lo que se hace es evaluar la función en el valor de "h", por lo que hay que haber encontrado "h" primero para posteriormente encontrar el valor de "k".
Para demostrar cómo se encuentra el vértice de una función se encontrará en la siguiente función: f(x) = 2x2 + 4x + 3. Al ver la función se puede observar que los términos de la función son: a = 2, b = 4 y c = 3.
- Primero se encuentra "h"
- h = -b2a
- h = -(4)2(2)
- h = 44
- h = -1
- Ahora se encuentra el valor de "k"
- k = f(h)
- k = 2(-1)2 + 4(-1) + 3
- k = 2 - 4 + 3
- k = 1
- Por lo tanto, las coordenadas (h, k) del vértice están en (-1, 1)
Dominio y rango de la función cuadrática
El dominio de una función cuadrática son los números reales, es decir, que el intervalo del dominio va desde menos infinito hasta más infinito: ]-∞, +∞[
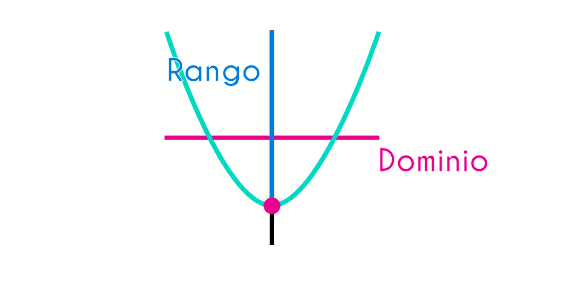
Para encontrar el rango de una función cuadrática, el proceso es un poco más complejo porque antes es necesario saber la posición del vértice, ya que dependiendo del vértice y de la dirección hacia donde se abre la parábola de la función cuadrática se definirá el rango de una función.
El vértice es el primer punto importante a la hora de determinar el rango de la función, porque este es el punto límite del rango. Este puede ser el límite inferior o el límite superior del rango, ya que el otro aspecto que define el rango es la dirección de la parábola, porque si la función se abre hacia arriba, entonces el rango irá desde la posición del vértice hasta más infinito, y en cambio, si la función abre hacia abajo, entonces el rango irá desde menos infinito hasta la posición del vértice.
Se tomará como ejemplo la función f(x) = x2 + 6. En este caso, el vértice está en (0, 6) y como el término "a" es positivo, entonces la parábola se abrirá hacia arriba, y el rango de esta función irá desde la coordenada "k" del vértice (6) hasta más infinito: [6, +∞[.
Forma General y Ecuación Canónica de la Función Cuadrática
La función cuadrática se puede expresar en dos formas principales: la forma general y la ecuación canónica. Cada una de estas formas tiene sus propias ventajas y aplicaciones en matemáticas y ciencias.
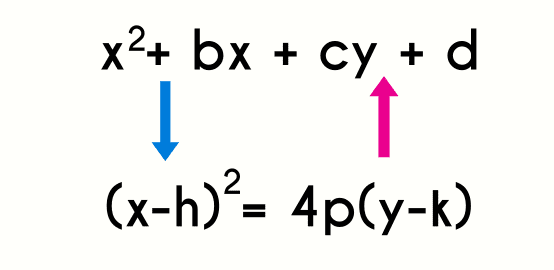
Forma General
La forma general de una función cuadrática es f(x) = ax2 + bx + c, donde "a", "b" y "c" son constantes. Esta forma es la más común y se utiliza para representar funciones cuadráticas en su forma original.
La forma general es útil para:
- Calcular las raíces de la función cuadrática utilizando la fórmula cuadrática.
- Identificar los coeficientes "a," "b" y "c" para determinar las características de la parábola, como la dirección de apertura y la posición del vértice.
- Realizar operaciones algebraicas y manipulaciones matemáticas para resolver ecuaciones cuadráticas.
Ecuación Canónica
La ecuación canónica de una función cuadrática toma la forma f(x) = a(x - h)2 + k, donde "a," "h," y "k" son constantes. Esta forma se utiliza para describir una parábola en función de su vértice (h, k) en lugar de los coeficientes tradicionales "a," "b" y "c".
La ecuación canónica es útil para:
- Identificar rápidamente el vértice de la parábola, que es una información crucial para comprender su posición en el plano cartesiano.
- Analizar la transformación de la parábola, como su traslación vertical u horizontal, sin necesidad de cálculos complicados.
- Visualizar de manera más intuitiva cómo la parábola se comporta a medida que los valores de "h" y "k" cambian.
Las dos formas, forma general y ecuación canónica, están relacionadas a través de transformaciones matemáticas. Las constantes "a," "h," y "k" en la ecuación canónica afectan la posición, el tamaño y la orientación de la parábola.
Historia de la Función Cuadrática
La función cuadrática ha desempeñado un papel fundamental en el desarrollo de las matemáticas y las ciencias a lo largo de la historia. Su origen se remonta a la antigua Babilonia, donde los matemáticos babilonios ya tenían conocimiento de ecuaciones cuadráticas. Posteriormente, los matemáticos griegos, como Euclides y Arquímedes, estudiaron y avanzaron en el entendimiento de las ecuaciones cuadráticas.
En la Edad Media, matemáticos como Al-Khwarizmi contribuyeron significativamente a la resolución de ecuaciones cuadráticas y desarrollaron métodos algebraicos para abordarlas. Durante el Renacimiento, matemáticos europeos como Viète y Descartes continuaron explorando las funciones cuadráticas y sus propiedades.
En la época moderna, las ecuaciones cuadráticas y las funciones cuadráticas se convirtieron en un pilar importante de las matemáticas y la física. La teoría de números, la mecánica newtoniana y la física cuántica utilizan ecuaciones cuadráticas en diversas aplicaciones. La función cuadrática también desempeña un papel clave en la teoría de optimización, la estadística y la ingeniería.
Hoy en día, las funciones cuadráticas son una parte esencial de la educación matemática y se utilizan en una amplia variedad de campos científicos y técnicos. Su importancia y relevancia en la historia de las matemáticas y las ciencias las convierten en una de las herramientas matemáticas más influyentes y versátiles.
Ejemplos de la función cuadrática
Ejemplo 1: Un coche que esta completamente quieto va a empezar a acelerar a razón de 4 metros por segundo, elaborar la función para este supuesto.
Para poder obtener la función de este problema se debe recurrir a las fórmulas del movimiento rectilíneo uniformemente variado, pero como este no es el tema de este artículo no se indagará más en el , pero la función que nos queda es la siguiente: f(x) = 2x2, una vez establecida la ecuación de la función, se procede a hacer lo demás.
Lo primero que se hará es encontrar las coordenadas del vértice de la parábola.
- Se encuentra la coordenada "x" del vertice (h)
- h = -(b)2(a)
- h = -(0)2(2)
- h = 04
- h = 0
- Y luego la coordenada "y" del vértice (k)
- k = f(h)
- k = 2(0)2
- k = 0
- Las coordenadas del vértice son (0,0)
Ahora que se tiene la posición del vértice se puede determinar que el dominio de esta función son los reales y el rango va desde 0 hasta más infinito. Y al graficar la función de posición de este problema queda de la siguiente manera.
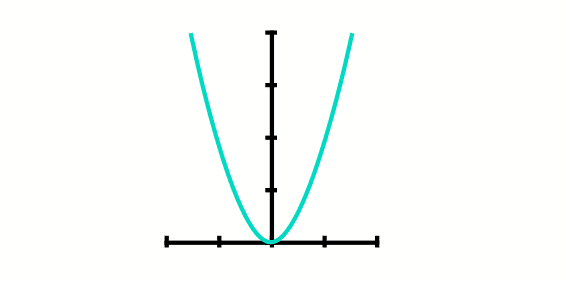
Ejemplo 2: Una colonia de hormigas se crece a razón de s2 + 1, donde “s” son semanas, graficar el crecimiento de la población de hormigas a partir de la semana 0 en adelante.
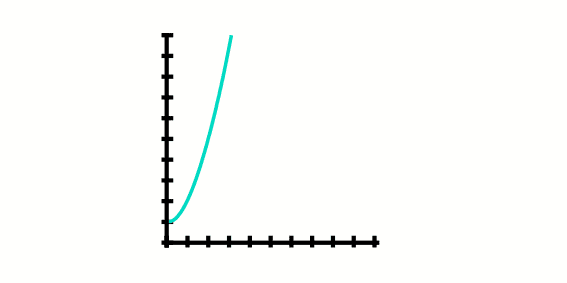
En este caso no se graficará toda la parábola, sino a partir de s=0 en adelante, por lo tanto en la gráfica no se podrá apreciar una parábola completa, pero si lo es solo que solo una parte.
En este problema lo que se hace es evaluar la función en las semanas que se quiera encontrar, en este caso será desde la semana 0 hasta la semana 4.
- f(s) = s2 + 1
- En la semana cero (al inicio de todo)
- f(0) = 02 + 1
- f(0) = 1
- En la primer semana
- f(1) = 12 + 1
- f(1) = 2
- En la segunda semana
- f(2) = 22 + 1
- f(2) = 5
- En la tercer semana
- f(3) = 32 + 1
- f(3) = 10
- En la cuarta semana
- f(4) = 42 + 1
- f(4) = 17
Conclusión
La función cuadrática es una herramienta poderosa en las matemáticas y las ciencias que desempeña un papel fundamental en la resolución de una amplia variedad de problemas. En este artículo, hemos explorado las diversas facetas de la función cuadrática, desde su forma general hasta su ecuación canónica, pasando por sus características clave como el vértice, la parábola y el dominio y rango.
Hemos descubierto cómo las funciones cuadráticas se aplican en la vida cotidiana y en campos profesionales, desde el modelado de trayectorias de proyectiles hasta la predicción de comportamientos económicos. También hemos explorado la rica historia de esta función y cómo se ha convertido en un pilar importante de las matemáticas y las ciencias a lo largo del tiempo.
Al comprender las diferentes formas de representar una función cuadrática y cómo aprovechar sus propiedades, los estudiantes y profesionales pueden abordar una amplia gama de problemas y tomar decisiones informadas en diversas disciplinas. La función cuadrática es una herramienta esencial que enriquece nuestra comprensión del mundo que nos rodea.
En resumen, la función cuadrática es una pieza fundamental en el rompecabezas de las matemáticas y las ciencias, y su versatilidad y aplicabilidad la convierten en un tema de estudio esencial para aquellos que buscan explorar y comprender el mundo cuantitativo que nos rodea.